Vivimos en la Era de la Información. El concepto de información es bastante abstracto y elusivo pero lo usamos con tanta familiaridad y tan cotidianamente que ni siquiera nos tomamos la molestia en definirla. Al menos sabemos 2 cosas básicas (o creemos 2 mitos básicos): que se constituye como el contenido del acto comunicativo y que es algo inmaterial (tal vez por la facilidad con que transita desde la boca al oído). La información emerge como contenido, como una especie de “cosa” u “objeto” pero con cualidades especiales: facilidad de reproducción, amplificación y propagación; pero a la vez intangible y volátil. Si tuviésemos que ponerle fecha de inicio, la Era de la Información comenzó el año 1948, poco tiempo después de finalizar la Segunda Guerra Mundial cuando Claude Shannon publicó el trabajo “Una Teoría Matemática de la Comunicación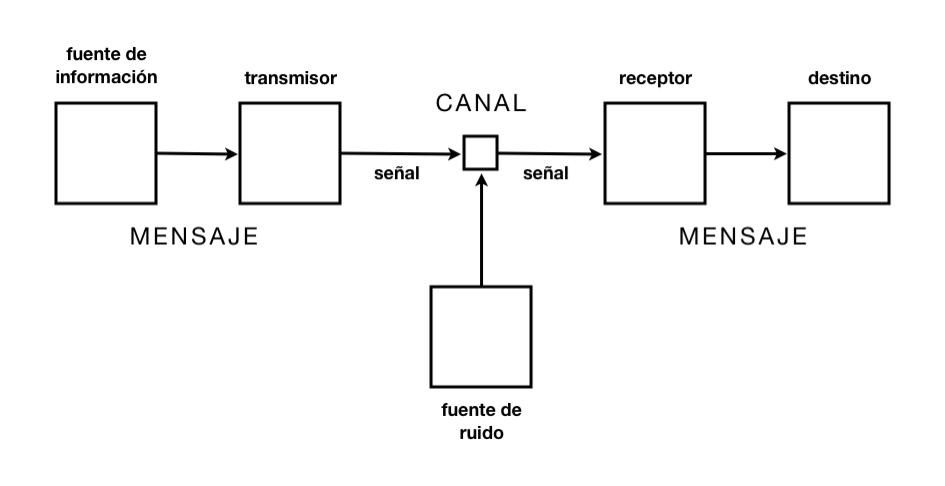” ((C.E. Shannon, “A Mathematical Theory of Communication“, Bell System Technical Journal, vol. 27, pp. 379-423, 623-656, July, October, 1948.)) . En este trabajo, Shannon define la información a partir de la relación entre señal y ruido; la información es una medida estadística de la incertidumbre del sistema (dentro de un sistema entrópico). La información implica una relación no-lineal y no-determinista entre los niveles micro y macroscópicos del sistema físico.

El problema fundamental de la comunicación consiste en reproducir en un punto exactamente (o con cierto grado de aproximación) un mensage seleccionado desde otro punto ((Ibid. pág. 1.))

Según el testimonio de investigadores (como Claude Shannon y Warren Weaver) trabajando para las compañias de telecomunicaciones ((en este caso, Bell Industries)) durante la primera mitad del siglo XX, la teoría de la información se ocupó fundamentalmente de la problemática de la reproducción de señales codificadas a través de un canal de manera rápida, económica y eficiente. Cuando una señal que viaja por un canal frecuentemente produce una estática de fondo. Esta estática no se resuelve simplemente amplificando la señal ya que esto sólo “inunda la señal en su propia energía”  y la vuelve indistinguible del ruido. El problema se resolvió parcialmente implementando distintos filtros, lo que volvió necesario desarrollar formas para codificar la señal de manera tal que minimizara los posibles errores producto del ruído y la distorsión. Entonces se desarrollaron códigos con patrones redundantes que sirvieran como verificación y corrección de la señal. Esto implicó una aproximación matemática-estadística al problema, un método que entendiera la información como una entidad separada de toda significación.

…”frecuentemente las señales tienen significado; esto es, se refieren o tienen correlación con un sistema compuesto por ciertas entidades físicas o conceptuales. Estos aspectos semánticos de la comunicación son irrelevantes para el problema de la ingeniería” ((Ibid. pág. 5.))

Es curioso ver que, visto desde este paradigma científico, un mensaje cargado de significación podría equivaler en términos estadísticos a otro completamente vacío e incoherente. Este pensamiento viene de una concepción biunívoca de la información; basta ver el esquema más arriba. No considera el modo multiunívoco del medio digital, mucho menos los efectos mediáticos del mensaje que ahora vive en un espacio de señales y protocolos abstractos, porque el contexto se constituye como un lugar. Estos efectos colaterales no podrían caer en la categoría de “ruido” definida por el modelo Shannon-Weaver. Otro aspecto significativo es el tipo de matemática que está involucrada para describir los fenómenos de la información. Se trata del modelo matemático de la termodinámica y la mecánica estadística ((El concepto de entropía tratado por Shannon es heredero directo del modelo Maxwell-Boltzmann para la descripción de los fenómenos termodinámicos que, por definición, no pueden hacerse cargo de precedir la ubicación de cada partícula sino que se describe las probabilidades del estado de determinado gas a un nivel macro.)). La entropía de un sistema, entonces, estará medida respecto al pordentaje de nuestra incertidumbre respecto de un determinado sistema de codificación o lenguaje ((La redundancia dentro de un lenguaje se mide como el índice de coincidencia. El IC en el idioma inglés es de 0.667 según William Friendman, “The Index of Coincidence and its Applications in Cryptography.”)). Entonces, a pesar de Shannon declaró que su teoría matemática de la información no guarda relación —o trabaja en un distinto nivel— respecto de la capa semántica, establece una relación directa entre la información y la entropía. Aplicaciones de esta mirada estadística las podemos observar en las cadenas de Markòv. Este mecanismo permite crear textos ((Texto entendido en el amplio sentido, ya que esta técnica se ha empleado para componer melodías dentro de un estilo, o crear publicaciones científicas completamente autómatas, por citar casos anecdóticos)) a partir de otros textos que funcionan como corpus referencial (Acá un ejemplo para hacer poemas). Google PageRank ((El algoritmo mediante el cual Google construye el ranking que entrega en los resultados de bísqueda.)) no es otra cosa que un conjunto inmenso de cadenas de Markòv en un grafo dirigido que está compuesto por toda la red. Cuando hablamos de SEO ((Search Engine Optimization: técnica para escribir los textos y disponer el código XHTML de una página para optimizar su visibilidad, por lo tanto rankeo, dentro de la lógica de los buscadores)), hablamos de escribir con el mayor grado de redundancia posible para que nos ubiquemos al centro del cluster semántico al cual queremos adscribir nuestro contenido. La pregunta es: dentro de un esquema estadístico de la visibilidad y la relevancia, ¿qué lugar tienen las particularidades (altamente entrópicas) ? ¿los puntos de vista excéntricos? ¿los folklorismos? ¿las cosas únicas y especiales? Ocurre que para medir el grado de entropía hay que recurrir a un corpus de referencia, ya que se trata de un valor puramente estadístico. Es decir, algo es frecuente o infrecuente, probable o improbable, de acuerdo a una cantidad enorme de casos catastrados como referencia. He ahí la falacia de la teoría: considerar un corpus lo suficientemente grande como para suponer un absoluto, un eje del sistema, es una fantasía. Primero, porque ni el lenguaje ni los medios, ni las conversaciones son estáticas; viven en su lenguajear. Segundo porque el corpus siempre será inexacto y tendrá muchos puntos ciegos. Desde ahí, la pregunta por la relevancia se vuelve mucho más compleja. De hecho, no vive en los extremos de la redundancia o la entropía.