// Hipótesis
(texto/palabras) = sintaxis
(hipertexto/texto) = metasintaxis

La sobreabundancia de información equivale a visualizar una trama. Cualquier palabra, o proceso, o forma empujada al límite de su potencial, invierte sus características y la vuelve una forma complementaria.
Marshall McLuhan

// también ver:
El texto y el tiempo (Axis Mundae), la continuidad de dimensiones en virtud de sus largos en el tiempo, con procesos irreversibles, del tipo:
En un Universo de n dimensiones existen (n (n-1))/2 relaciones bidireccionales

Paisajes de Papel

En su búsqueda por visualizar espacios extra dimensionales, el matemático alemán Georg Riemann desarrolló una metáfora muy sencilla: dos hojas de papel -cada una representando un universo bidimensional- pegadas en un pequeño tramo lineal ubicado al centro de cada hoja. Vistas en corte serían dos hipérbolas cuyas curvas se encuentran en el centro. Luego imaginó a un ser bidimensional transitando de una hoja a la otra pasando por este tajo - abertura. Este tránsito consiste, efectivamente en un salto extra - dimensional: se ha movido de un mundo a otro con las mismas leyes, a otra "planilandia". Quizá, este ser está desorientado porque el paisaje ha cambiado a pesar de la coherencia lineal de su traslado. Para un espectador tridimensional, quizá pueda haberse reflejado, pero para este ser bidimensional, este planilandés, este reflejo no es perceptible. Este tránsito momentáneamente ha creado la tercera dimensión que paradójicamente consiste en un tajo vacío y carente de espacio concreto.

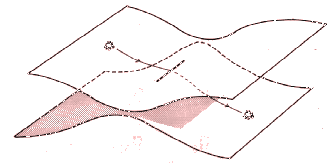
Este ejemplo llevado a la vida cotidiana: Al subir a un ascensor, nosotros nunca vemos el conducto vertical de ascenso, a pesar de ello, sabemos por un proceso de inferencia que nos hemos movido algo puesto que el paisaje cambia ostensiblemente cuando las puertas del ascensor de reabren.

Primero: Cabe reconocer la desventaja del texto escrito para traer una presencia espacial respecto de una imagen. Esta diferencia, coyuntural en el debate del hipertexto, ha diferenciado desde siempre a las artes verbales de las artes visuales.

Segundo y más importante: este modelo de representación de dos universos planos y paralelos conectados por este "agujero negro de cero largo" es un modo de visualizar la vinculación de los textos. La física lo llama "superficie multiconectada", en la lectura se llama "hipertexto".
Los textos impresos son "planilandia". La interfaz natural para los textos son nuestros ojos, que se mueven de izquierda a derecha, de arriba hacia abajo pero nunca, a través. Podemos físicamente dar vuelta a la página pero este acto resulta periférico a la continuidad textual, es un requerimiento físico que apela a la finitud del formato página: la sintaxis interna del texto le da igual valor al carácter"espacio" que a dar vuelta a la página. (incluso, yendo más lejos, lo podríamos representar linealmente).
La presencia de hipervínculos en la continuidad del texto interfiere y varía la continuidad sintáctica. La opción estética del hipertexto apela a estas posibilidades de irrupción, tanto temática como estructuralmente. Al modo de este tajo en planilandia, los vínculos le suman una coordenada espacial a este medio primordialmente temporal, abriendo una panorama de posibilidades al autor. El acto de traspasar por estos vínculos siendo una continuidad interna del lenguaje, esencialmente crea espacio.

Topología y Lectura

La Topología es una rama de las matemáticas que normalmente no hace ninguna referencia a los números, podríamos decir que su campo es "no numérico".

Para un topólogo un espacio de hipertexto se vería como un conjunto de puntos, o mejor dicho, nodos conectados por vínculos.

        I + - - - - - - - - - - + 1
            - _                   |
                 - _              |
                      - _         |
                          - _     |
                              - _ |
                                + 2

        <- [Sup. o Índice]
                   Cap.1 ->
   Índice + - - - - - - - - - - + Cap.1
             - _                  |
                 - _              | [Previo
           [Sup.]    - _          | o Ant.]
                         - _      | [Sig.]
                     Cap.2   - _  |
                                  + cap.2

Aunque este esquema construye un triángulo, los topólogos (a diferencia de los geómetras) no se interesan por el largo que puedan tener estos vínculos o los ángulos que formen entre sí; sólo que hay tres nodos y que cada uno está conectado con el otro.

En hipertexto, estos nodos serán documentos, por ejemplo, un índice y dos capítulos. En este es el ejemplo más básico pero nótese que el vínculo entre dos nodos cualquiera variará su nombre dependiendo de la dirección.
En este caso, siempre el vínculo más problemático es el "Prev." o previo, puesto que queda difuso el criterio de su nombre, si se trata de un criterio temporal (de la lectura, lo que leí antes) o de la estructura editorial (el capítulo previo). Normalmente, en el hipertexto, existe un divorcio entre estas dos posibilidades.

Esto obliga a aumentar la cantidad de indicaciones y vínculos (Anterior, Siguiente, Superior, Índice general, etc.) y se comienza a hilvanar un "espacio" de lectura donde hay distintos horizontes y niveles de profundidad, artículos periféricos y ejes centrales. Esto es lo que comúnmente se llama en internet "mapa del sitio" donde se visualiza la totalidad de niveles y subniveles expresados jerárquicamente en una figura. La disciplina que concibe esta figura y se ocupa de las relaciones topológicas cuidando la orientación del lector se llama arquitectura de la información